https://github.com/cuttingworms/Data-Structures-with-Python
GitHub - cuttingworms/Data-Structures-with-Python
Contribute to cuttingworms/Data-Structures-with-Python development by creating an account on GitHub.
github.com
- 2-3-4 트리 혹은 (2, 4) 트리
- 내부 노드의 차수가 2, 3, 4인 완전 균형 탐색 트리
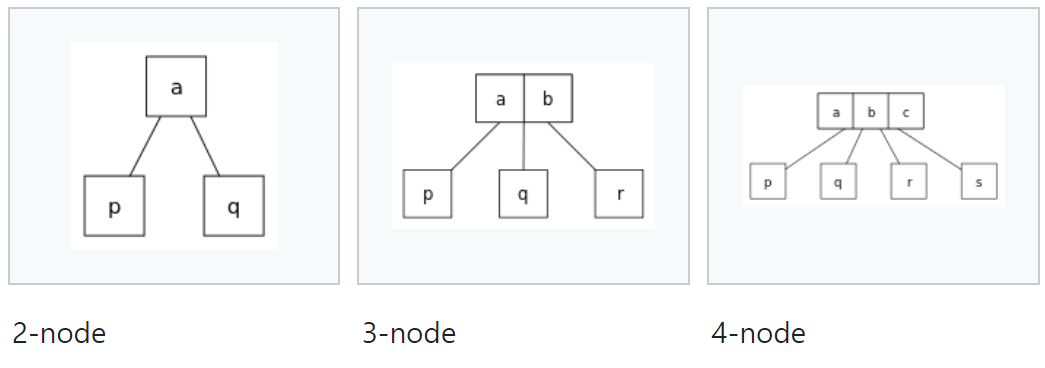
- 2-노드 : 한 개의 키 a를 가지며 자식 노드는 2개
- p.key <= a.key <= q.key
- 3-노드 : 두 개의 키 a, b를 가지며 자식 노드는 3개
- p.key <= a.key <= q.key <= b.key <= r.key
- 4-노드 : 세 개의 키 a, b, c를 가지며 자식 노드는 4개
- p.key <= a.key <= q.key <= b.key <= r.key <= c.key <= s.key
- 2-노드 : 한 개의 키 a를 가지며 자식 노드는 2개
- 특징
- 모든 단말 노드에 이르는 경로의 길이가 같음
- 모든 단말 노드가 같은 깊이에 존재하는 완전 균형 트리
- 2-3-4 트리가 2-노드로만 구성되면 포화 이진 탐색 트리
- 2-3-4 트리의 일반화된 중위 순회 결과는 키 값이 정렬된 결과를 얻음
- 노드에 저장되는 키의 수가 달라 구현이 복잡
- 높이
- n개의 키를 갖는 2-3-4 트리의 높이는 O(log(n))
- 모든 노드가 2-노드일 때 최대 높이
- 모든 노드가 4-노드일 때 최소 높이
- 연산
- Insertion
- 새로운 키 k를 삽입하기 위하여 탐색을 수행한 후, 단말 노드의 적절한 위치(정렬된 순서가 유지되는)에 키 k를 추가
- Overflow 발생의 가능성 있음 : 노드의 키가 4개가 되어 5-노드가 되는 상태
- Split : Overflow 노드의 중간값(median)을 선택하여 부모 노드로 올려 보내고, Overflow 노드는 2-노드와 3-노드로 분리, 후에 부모 노드에서 Overflow 발생 시 같은 일을 반복
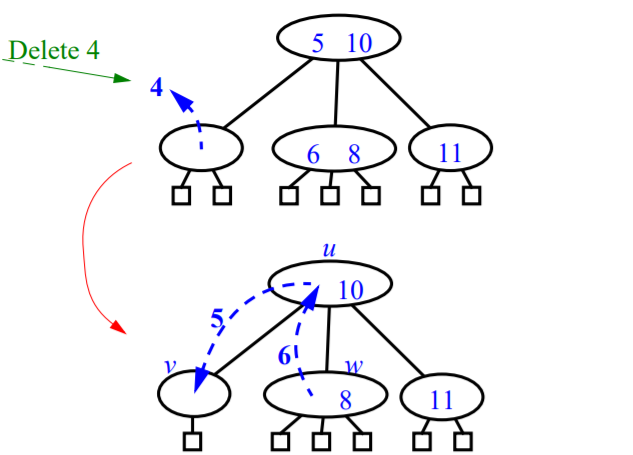
- Deletion
- 키 k를 삭제하기 위하여 탐색을 수행
- 실제 삭제는 단말 노드에서 이뤄짐
- 내부 노드에서 키가 발견되는 경우, 중위 후속자 또는 중위 선행자와 교환 후 단말 노드에서 삭제함
- Underflow 발생의 가능성 있음 : 노드의 키가 0개가 되는 상태
- Transfer : 삭제된 노드의 형제 노드가 3-노드 혹은 4-노드일 경우
- 형제 노드의 키 값(왼쪽 형제의 최댓값 혹은 오른쪽 형제의 최솟값)으로 부모를 밀어내며 전달 받음
- Fusion : 삭제된 노드의 형제 노드가 모두 2-노드인 경우
- Underflow 노드와 형제 노드를 하나의 노드로 병합하고, 두 노드의 분기점 역할을 하던 부모 노드의 키를 병합된 노드의 키로 내리는 연산
- Fusion 연산이 부모 노드를 Underflow로 만들 수 있음 : 루트에 이르는 동안 Fusion 연산을 반복하여 수행
- Transfer : 삭제된 노드의 형제 노드가 3-노드 혹은 4-노드일 경우
- Insertion

- 레드-블랙 트리 (Red-Black Tree)
- 2-3-4 트리를 이진 탐색 트리로 표현한 트리
- 노드에 색상 정보를 추가 : Red 또는 Black
- 특징
- Root 노드는 블랙 노드
- None 노드는 블랙 노드
- 레드 노드의 자식 노드는 항상 블랙 노드
- 모든 단말 노드는 같은 블랙 깊이(Black depth)를 가짐
- 연산
- Insertion
- 이진 탐색 트리와 동일한 삽입 연산을 수행
- 단, 삽입되는 노드는 반드시 레드 노드
- 레드-블랙 트리의 속성을 유지
- 삽입된 레드 노드의 부모 노드가 레드 노드인 경우 : Double-red
- 부모 노드의 형제 노드가 없거나 블랙인 경우 : Rotation
- 부모 노드의 형제가 레드일 때 : Recoloring
- 이진 탐색 트리와 동일한 삽입 연산을 수행
- Deletion
- 이진 탐색 트리와 동일한 삭제 연상을 수행
- 레드-블랙 트리의 속성을 유지
- Insertion
- (2, 4) 트리 & 레드-블랙 트리의 수행 시간
- 완전 균형 탐색 트리이기 때문에 높이가 O(log(n))이므로 탐색, 삽입, 삭제에 O(log(n)) 소요
'자료구조 (Data Structures) > 트리, Tree' 카테고리의 다른 글
| [Tree] B-트리, B-Tree (0) | 2022.01.12 |
|---|---|
| [Tree] AVL 트리, AVL Tree (0) | 2022.01.11 |
| [Tree] 탐색 트리, Search Tree (0) | 2022.01.11 |
| [Tree] 이진 힙, Binary Heap (0) | 2022.01.11 |
| [Tree] 이진 트리, Binary Tree (0) | 2021.12.31 |



